What Is the Collatz Conjecture Sequence Generator and How to Use It

Mathematics has long been filled with fascinating mysteries — some solved, some still awaiting their breakthroughs. Among the most famous unsolved problems that continues to intrigue both mathematicians and enthusiasts alike is the Collatz Conjecture. Despite its simple formulation, it hides a mesmerising complexity that seems to defy easy explanation.

The Collatz Conjecture Sequence Generator is a tool designed to bring this mathematical wonder to life. By entering any positive integer, users can instantly see the sequence of numbers that the Collatz process produces, step by step, until it eventually reaches the number 1. This interactive tool helps students, educators, and math enthusiasts visualise one of mathematics’ most elegant yet mysterious patterns.

In this article, we’ll explore what the Collatz Conjecture is, how the sequence works, and how to use the Collatz Conjecture Sequence Generator to better understand this fascinating concept.

What Is the Collatz Conjecture?

The Collatz Conjecture, also known as the 3n + 1 problem, is a mathematical hypothesis proposed by the German mathematician Lothar Collatz in 1937. The idea is simple enough for a child to understand, yet no one has been able to prove it true for all numbers.

Here’s how it works:

1. Start with any positive integer, n.
2. If the number is even, divide it by 2.
3. If the number is odd, multiply it by 3 and add 1.
4. Repeat the process with the resulting number.

The conjecture states that no matter what positive integer you start with, the sequence will always eventually reach 1.

For example:
If you start with 6, the sequence goes like this:
6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1

Simple, right? But here’s the catch: while this pattern has been verified by computers for extremely large numbers — even up to 2⁶⁸ (that’s over 295 billion billion!) — no one has been able to mathematically prove that it always works for all positive integers.

That’s where tools like the Collatz Conjecture Sequence Generator become both educational and entertaining.

What Is the Collatz Conjecture Sequence Generator?

The Collatz Conjecture Sequence Generator is an online tool that automatically calculates and displays the sequence generated by the Collatz rules for any number you enter.

It’s a simple yet powerful way to visualize how the conjecture behaves in real time. Instead of manually performing the steps (which can take a while for larger numbers), this generator instantly computes the full chain of numbers and often displays it as a clean, easy-to-read sequence.

Some advanced versions of the tool even include:

• Step-by-step animations showing each transformation.
• Graphs visualizing how the numbers rise and fall.
• A count of how many steps it takes to reach 1.

This turns a pure mathematical idea into a hands-on learning experience that anyone can understand and explore.

Why the Collatz Conjecture Is So Fascinating

What makes the Collatz Conjecture so interesting is how deceptively simple it appears. The rules are easy enough to code in a few lines of JavaScript, yet the underlying behavior of the numbers has stumped the world’s greatest mathematical minds for decades.

Patterns appear to emerge and disappear as numbers rise and fall in unpredictable ways. Some sequences soar into large numbers before quickly collapsing back to 1, while others stay low and steady. It’s a chaotic yet mesmerizing dance that seems to hint at deep mathematical order — one we haven’t fully grasped yet.

This paradox — simplicity in definition, complexity in behavior — is what keeps mathematicians coming back to the Collatz problem. The Collatz Conjecture Sequence Generator lets you witness this complexity firsthand.

How to Use the Collatz Conjecture Sequence Generator

Using the generator is incredibly straightforward, even if you have no background in mathematics. Here’s how it typically works:

1. Open the tool. You’ll see a clean interface with a single input field labeled something like “Enter a Number.”
2. Enter any positive integer. For example, type in 11.
3. Click the “Generate Sequence” button.
4. The tool will automatically calculate and display each step of the Collatz sequence for that number.
5. You’ll then see a list like this:
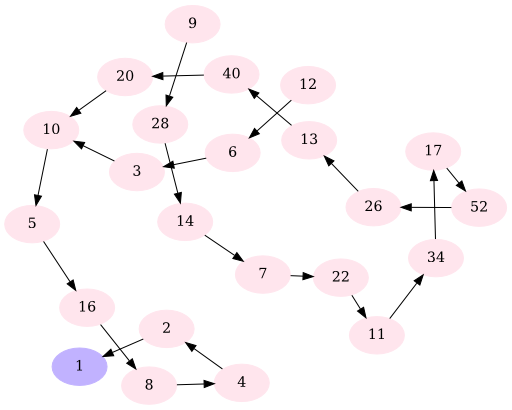
   11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
6. Some versions also display the total number of steps (in this case, 14) before reaching 1.

That’s it! You’ve just watched the Collatz Conjecture in action.

If you try entering different numbers — like 7, 25, or even 1000 — you’ll notice that each sequence follows its own unique path, but every single one will eventually end at 1.

How It Helps You Learn

For students, teachers, and lifelong learners, the Collatz Conjecture Sequence Generator offers several educational benefits:

• Visualisation: Seeing the sequence displayed step-by-step makes the process easier to understand.
• Pattern Recognition: You can explore how certain numbers behave differently and whether any patterns emerge.
• Interactivity: The ability to test multiple inputs encourages curiosity and engagement.
• Understanding recursion and iteration: For those learning programming or mathematics, this is an excellent example of how iterative logic works in practice.

By using this generator, abstract mathematical theory becomes tangible and interactive — an experience that deepens comprehension far more effectively than reading about it alone.

Fun Ways to Experiment

Once you start using the Collatz Conjecture Sequence Generator, it’s hard to stop experimenting. Here are a few fun ways to make the most of it:

• Compare sequences: Try entering two consecutive numbers (like 15 and 16) and see how different their sequences are before they reach 1.
• Find long sequences: Some numbers take surprisingly many steps to reach 1. See if you can find a number that produces an unusually long sequence.
• Visualise patterns: Use the tool’s graphing feature (if available) to watch the numbers rise and fall.
• Teach others: It’s a great conversation starter or classroom demonstration for showing how simple rules can lead to complex outcomes.

The Ongoing Mystery

Despite being tested for trillions of numbers with computers, the Collatz Conjecture remains unproven. In fact, it’s so difficult that mathematician Paul Erdős once famously said, “Mathematics is not yet ready for such problems.”

And yet, that’s precisely what makes this topic — and tools like the Collatz Conjecture Sequence Generator — so captivating. Each time you run the generator, you’re exploring a little piece of mathematical mystery, participating in a phenomenon that continues to challenge even the best minds in the world.

Conclusion

The Collatz Conjecture Sequence Generator is more than just a fun interactive math tool — it’s a window into one of the most puzzling unsolved questions in mathematics. By turning numbers into visible, understandable sequences, it helps people grasp both the simplicity and complexity of this timeless conjecture.

Using it is effortless: you enter a number, press a button, and watch the magic unfold. But behind that simple interaction lies one of the greatest unsolved mysteries in all of mathematics — a sequence that seems to always end at 1, but still refuses to be proven.

Whether you’re a math lover, a student, or simply curious about how patterns emerge from simple rules, the Collatz Conjecture Sequence Generator is an engaging way to explore the beauty of mathematical chaos. It’s proof that even in the most straightforward formulas, there’s always room for mystery, wonder, and endless discovery.